AIのJavascript ―演算なしでパスの交点を抽出―
で、つぶやいたの貼っておきます。何かと言うと、ジオメトリ演算皆無の交点検出スクリプトです。コンセプトコードですので、実際の運用には例外処理が必要です。アンカーポイントで交差している場合とか…
こちらがコードです。
var pt = [];
var rslt = [];
var tg = app.selection;
var i,j;
for (j=0;j<2;j++){
for (i=0;i<app.selection[j].pathPoints.length;i++){
pt.push(app.selection[j].pathPoints[i].anchor);
}
}
var gp = app.activeDocument.groupItems.add();
tg[0].duplicate(gp,ElementPlacement.PLACEATEND);
tg[1].duplicate(gp,ElementPlacement.PLACEATEND);
gp.selected = true;
app.executeMenuCommand("Live Pathfinder Add");
app.executeMenuCommand('expandStyle');
for (i=0;i<app.selection[0].pathItems[0].pathPoints.length;i++){
rslt.push(app.selection[0].pathItems[0].pathPoints[i].anchor);
}
for (i=0;i<pt.length;i++) {
for (j=0;j<rslt.length;j++){
if (pointDiff (pt[i], rslt[j])){
rslt.splice(j, 1);
break;
}
}
}
if (rslt.length>0) {
var pth = app.activeDocument.pathItems.add();
var pts;
for (i=0;i<rslt.length;i++) {
pts = pth.pathPoints.add();
pts.anchor = rslt[i];
pts.leftDirection = rslt[i];
pts.rightDirection = rslt[i];
}
}
app.selection[0].remove();
function pointDiff (a,b){
if (a[0]==b[0]&&a[1]==b[1]) return true;
return false;
}ご覧のとおりです。先日のパスファインダースクリプトがベースになります。事前にunionかけるpathItemのpathPointのanchorを全て配列に収容しておき、union後のpathPointのanchorと比較し、新たに生成されたポイントをチェックします。この新しいアンカーポイントが交点となります。
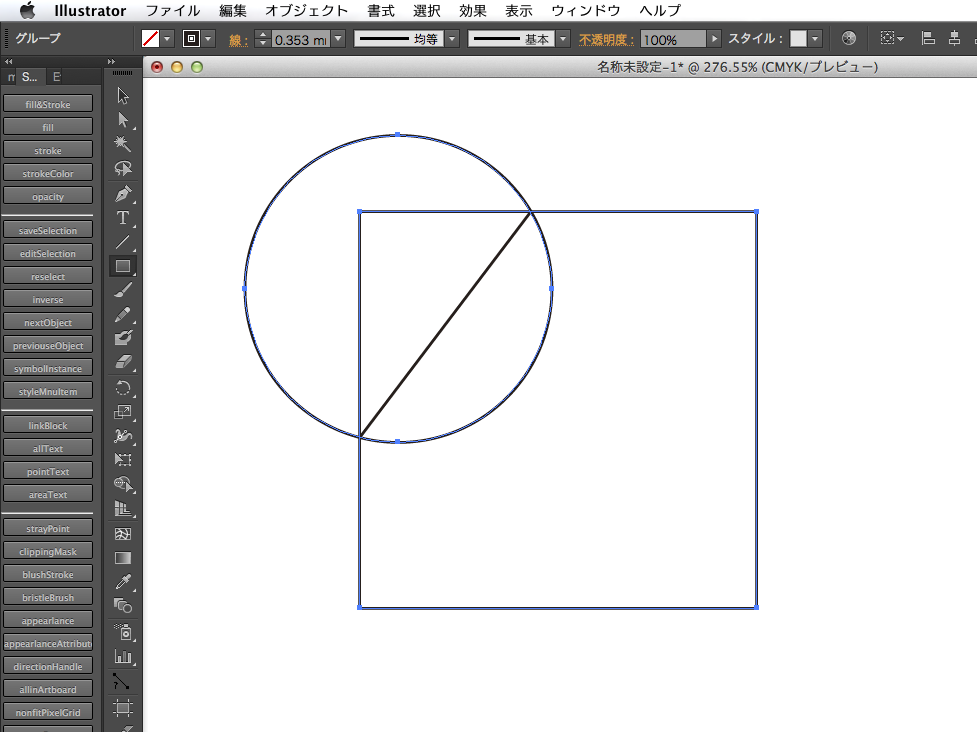
この例では検出した交点を線分で接続してみました。例外処理を含む実用的なのはそのうちにwww
3件のフィードバック
コメントを残す
コメントを投稿するにはログインしてください。






コメント失礼致します。
パスとパスの交点を起点として下へ垂直に5mmの線を引くスクリプトを探しており、こちらを見つけました。ご紹介くださっているスクリプトの応用で可能なものでしょうか?
お手数お掛けしますが、お時間ございます時にお返事頂ければ幸いです。どうぞ宜しくお願い致します。
比較する対象をanchorだけではなくleftDirection及びrightDirectionも同時に比較するようにするとある程度は検出可能ですが、ここにオープンパスが絡んでくる場合、パスファインダー処理を行うと閉図形となるために色々と面倒になってきます。という事で、この手法が利用可能なのはそういった例外を生じる部分をどう排除するかがキモとなります。
正攻法で行くとある特定のベジェ曲線の区間が好転を含むかどうかを判断するには以前説明したカーブを任意の比率で分割する関数等を利用して曲線上の任意の点を得ながら二分法を利用して追い込むような処理が必要となります。アルゴリズムの良し悪しである程度は実行速度が良くなりますが、反復回数の多いコードとなりますからスクリプトでの処理は不利なものです。
検索では中々見つからないと思いますが、これはそういった事情があるためで、難易度の高い処理のひとつです。
処理について詳しくご解説くださりありがとうございました。素人ですので、コピーしてパスファインダー使用で交点にポイントを付け、その座標を起点として簡単に垂直に線が引けないものかと考えました。
これが可能なら図面の整合の
作業効率が上がると思いましたが、
中々難しい問題なんですね。
ありがとうございます。