ボロノイ図を描くスクリプトのチューニング

前のChatGPTさんに丸投げしたボロノイ図のチューニングについてはIllustrator向きではない処理を無理やり実装して失敗しました。ということで、チューニングの方向性が間違っているのは明白なので他の方法を考えます。
なにが問題かというと、デロネー条件を判定するための三角形を用意するところに処理の大半の負荷が存在しています。ここのデロネー三角分割を何とかするのが最適解に連なる道と考えたわけです。
今回はこの部分をボイヤー・ワトソンのアルゴリズムを利用してデロネー三角分割を行うことにします。
ボイヤー・ワトソンのアルゴリズムについて
●各点を追加する際に、デロネー条件を満たさない三角形を削除し、新たに三角形を作成する。
●計算量は平均 O(n・log n) で実用的。
以下、手順です。
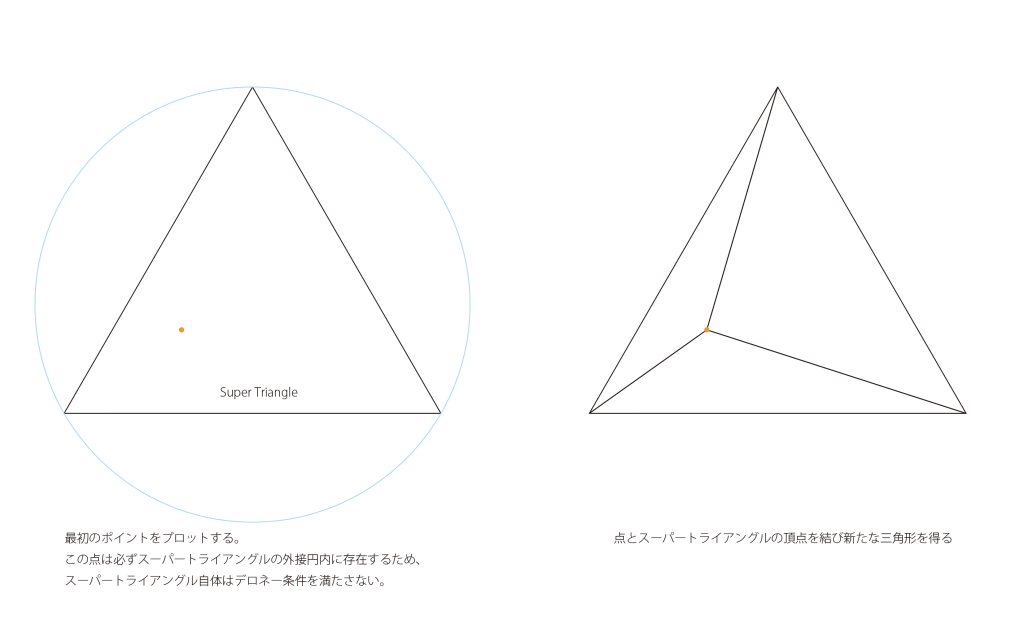
- スーパートライアングル(すべての点を内包する非常に大きな三角形)を作成し、それを三角形のリストに加える
- 最初の点をプロットする。この最初の点は必ず三角形のリストの最初のもの(スーパートライアングル)の外接円内に存在するため、当該三角形はデロネー条件を満たさない。なので三角形のリストから外す。この三角形の辺と追加した点を利用して新たな三角形を生成し、リストに加える。
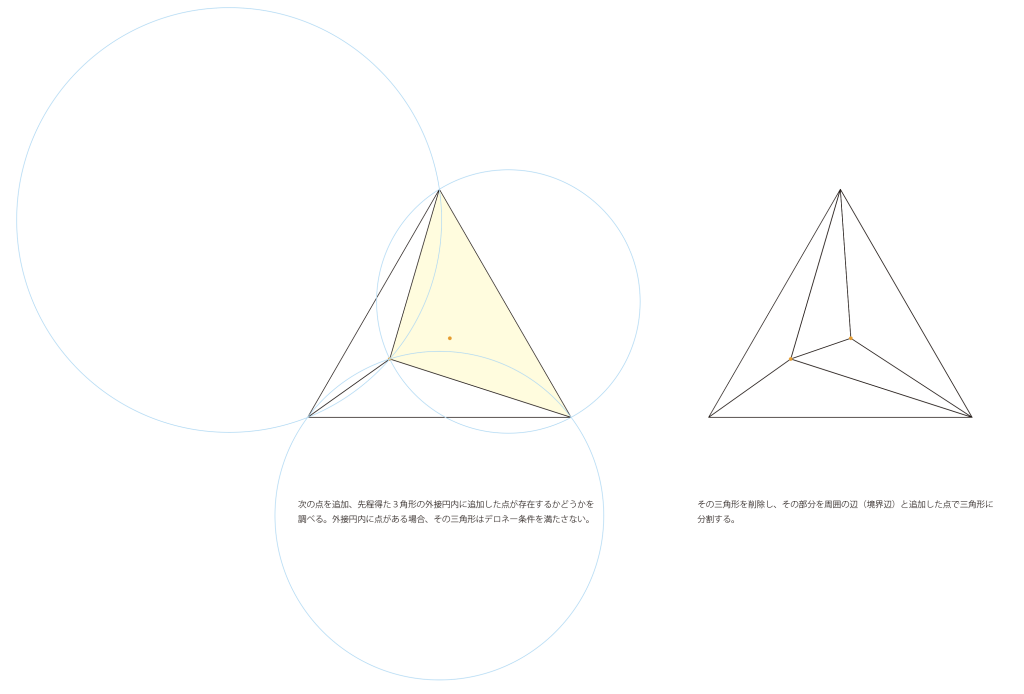
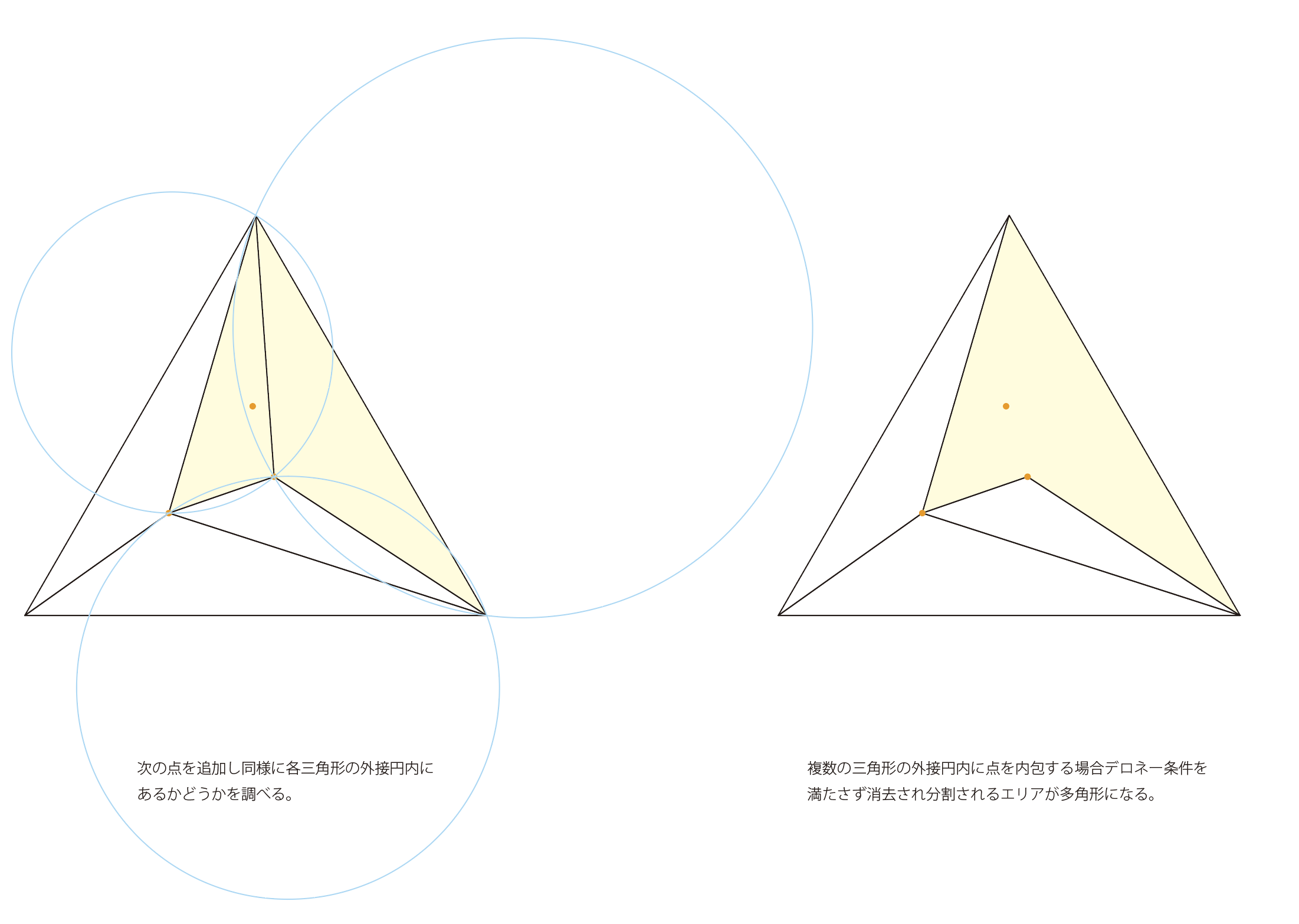
- 次の点をプロットし、各三角形の外接円内に入るかどうかを確認する。外接円内に点が存在する場合はデロネー条件を満たさないので、その三角形をリストから除外する。隣接する複数の三角形が除外された場合、その除外されたエリアは多角形を形成する。
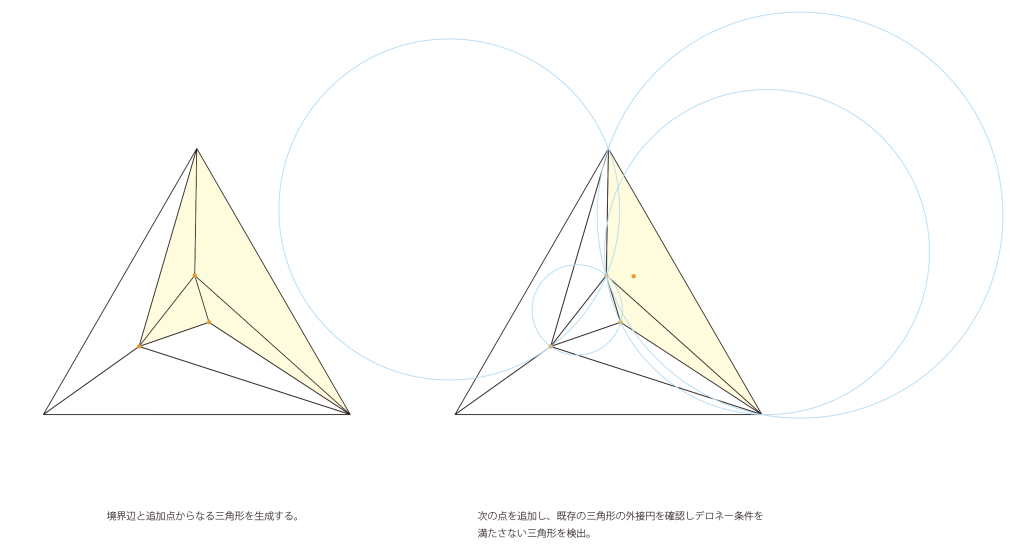
- 除外されたエリアの辺と追加された点を利用して新たな三角形を生成しリストに加える。
- 3〜4を最後の点まで繰り返し、最後にスーパートライアングルの頂点を含む三角形をリストから除外するとリストに残る三角形はデロネー条件を満たすものだけとなります。
一応、図も用意しました。
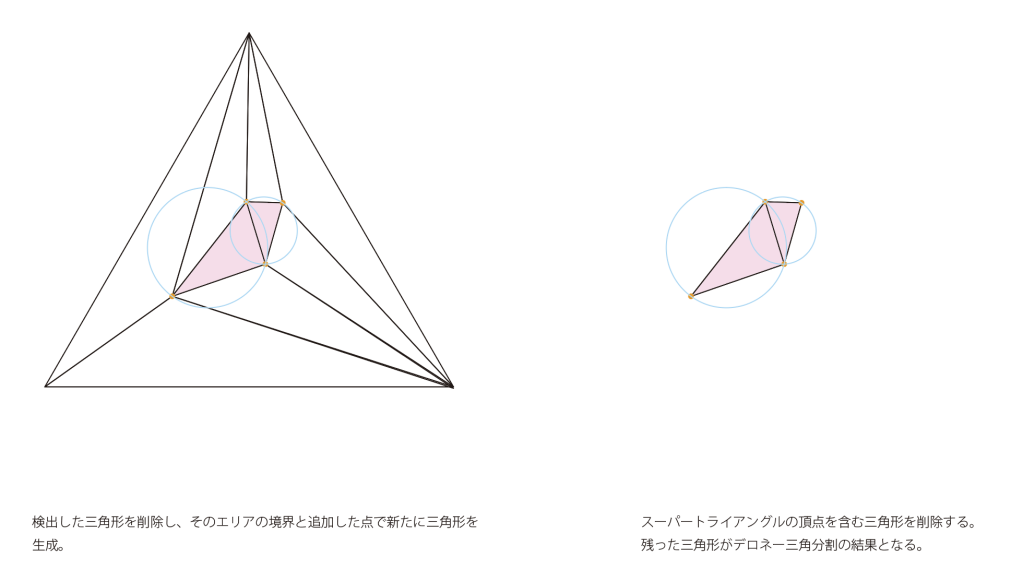
このように任意の位置に点がプロットされるため最大で計算量はO(n^2)になる可能性がありますが、平均で考えるとO(n・log n)となります。
以上がボイヤー・ワトソンのアルゴリズムによるデロネー三角分割です。以前の総当たりのアルゴリズムは3重ループだったのでO(n^3)という膨大な計算量をこなす必要がありました。例えば100個の点が存在する場合、最大100万というループ処理が生じます。一方このボイヤー・ワトソンのアルゴリズムでは平均計算量で考えると700回弱、最悪計算量でもn^2の10000回の計算で済むということになります。
という事で、以下のスクリプトでボロノイ図を描くと以前の処理と比較してかなり高速に処理できます。また、メモリリーク等の影響も小さくなることから4000点程度まで安定して作図可能です。ちなみに、以前のものでは500点プロットさせると延々とIllustratorがぐるぐるします。
var numPoints = 4000;
var lyr = app.activeDocument.layers.add();
lyr.name = "Voronoi";
var wd = 800;
var ht = 800;
var points = [];
for (var i=0; i<numPoints; i++)
{
var x = Math.random() * wd;
var y = Math.random() * ht;
points.push([x, y]);
}
// Super Triangle
var superTriangle = [[-4000, -4000], [4000, -4000], [0, 6928]];
var triangles = [superTriangle];
// Get Circumcircle
function circumcircle(a, b, c)
{
var d = 2 * ((a[0] - c[0]) * (b[1] - c[1]) - (b[0] - c[0]) * (a[1] - c[1]));
var ux = ((a[0] * a[0] + a[1] * a[1]) * (b[1] - c[1]) +
(b[0] * b[0] + b[1] * b[1]) * (c[1] - a[1]) +
(c[0] * c[0] + c[1] * c[1]) * (a[1] - b[1])) / d;
var uy = ((a[0] * a[0] + a[1] * a[1]) * (c[0] - b[0]) +
(b[0] * b[0] + b[1] * b[1]) * (a[0] - c[0]) +
(c[0] * c[0] + c[1] * c[1]) * (b[0] - a[0])) / d;
var center = [ux, uy];
var radiusSq = (a[0] - ux) * (a[0] - ux) + (a[1] - uy) * (a[1] - uy);
return { center: center, radiusSq: radiusSq };
}
// Get the edge of a triangle
function getEdges(triangle)
{
return [
[triangle[0], triangle[1]],
[triangle[1], triangle[2]],
[triangle[2], triangle[0]]
];
}
// edge equation
function edgeEquals(e1, e2)
{
return (e1[0][0]===e2[0][0] && e1[0][1]===e2[0][1] && e1[1][0]===e2[1][0] && e1[1][1]===e2[1][1]) ||
(e1[0][0]===e2[1][0] && e1[0][1]===e2[1][1] && e1[1][0]===e2[0][0] && e1[1][1]===e2[0][1]);
}
// Bowyer-Watson algorism
function triangulate(points)
{
var triangles = [superTriangle];
for (var i=0; i<points.length; i++)
{
var point = points[i];
var badTriangles = [];
// Find a triangle with a point inside the circumscribed circle
for (var j = 0; j < triangles.length; j++)
{
var circ = circumcircle(triangles[j][0], triangles[j][1], triangles[j][2]);
var distSq = (point[0] - circ.center[0]) * (point[0] - circ.center[0]) +
(point[1] - circ.center[1]) * (point[1] - circ.center[1]);
if (distSq<circ.radiusSq)
{
badTriangles.push(triangles[j]);
}
}
// Get the edge of the removed triangle
var boundaryEdges = [];
for (var j=0; j<badTriangles.length; j++)
{
var edges = getEdges(badTriangles[j]);
for (var k=0; k<edges.length; k++)
{
var shared = false;
for (var l=0; l<boundaryEdges.length; l++)
{
if (edgeEquals(edges[k], boundaryEdges[l]))
{
shared = true;
boundaryEdges.splice(l, 1);
break;
}
}
if (!shared) boundaryEdges.push(edges[k]);
}
}
// remove badTriangles
var newTriangles = [];
for (var j=0; j<triangles.length; j++)
{
var isBad = false;
for (var k=0; k<badTriangles.length; k++)
{
if (triangles[j]===badTriangles[k]) {
isBad = true;
break;
}
}
if (!isBad) newTriangles.push(triangles[j]);
}
triangles = newTriangles;
// 新Create a new triangle
for (var j=0; j<boundaryEdges.length; j++)
{
triangles.push([boundaryEdges[j][0], boundaryEdges[j][1], point]);
}
}
// Delete triangles tangent to super triangles
var finalTriangles = [];
for (var i=0; i<triangles.length; i++)
{
var t = triangles[i];
if (t[0]!==superTriangle[0] && t[1]!==superTriangle[0] && t[2]!==superTriangle[0] &&
t[0] !== superTriangle[1] && t[1]!==superTriangle[1] && t[2]!==superTriangle[1] &&
t[0] !== superTriangle[2] && t[1]!==superTriangle[2] && t[2]!==superTriangle[2])
{
finalTriangles.push(t);
}
}
return finalTriangles;
}
// Draw Delaunay triangles
function drawDelaunay(layer, triangles)
{
var red = new CMYKColor();
red.cyan = 0;
red.magenta = 100;
red.yellow = 0;
red.black = 0;
for (var i = 0; i < triangles.length; i++)
{
var path = layer.pathItems.add();
path.setEntirePath([triangles[i][0], triangles[i][1], triangles[i][2], triangles[i][0]]);
path.stroked = true;
path.strokeColor = red;
path.strokeWidth = 0.3;
path.filled = false;
}
}
// draw Voronoi diagram
function drawVoronoi(lyr, triangles)
{
var black = new GrayColor();
black.gray = 100;
var circumcenters = [];
for (var i=0; i<triangles.length; i++)
{
circumcenters.push(circumcircle(triangles[i][0], triangles[i][1], triangles[i][2]));
}
for (var i=0; i<triangles.length; i++)
{
for (var j=i+1; j<triangles.length; j++)
{
var sharedVertices = 0;
for (var v1=0; v1<3; v1++)
{
for (var v2=0; v2<3; v2++)
{
if (triangles[i][v1][0]===triangles[j][v2][0] &&
triangles[i][v1][1]===triangles[j][v2][1]) sharedVertices++;
}
}
if (sharedVertices===2)
{
var pth = lyr.pathItems.add();
pth.setEntirePath([circumcenters[i].center, circumcenters[j].center]);
pth.stroked = true;
pth.strokeColor = black;
pth.strokeWidth = 0.3;
pth.filled = false;
}
}
}
}
function drawPoints(layer, points)
{
var red = new CMYKColor();
red.cyan = 0;
red.magenta = 100;
red.yellow = 100;
red.black = 0;
for (var i=0; i<points.length; i++)
{
var ellipse = layer.pathItems.ellipse(
points[i][1] + 1, points[i][0] - 1, 2, 2);
ellipse.stroked = false;
ellipse.filled = true;
ellipse.fillColor = red;
}
}
//
var triangles = triangulate(points);
//drawDelaunay(lyr, triangles);
drawVoronoi(lyr, triangles);
drawPoints(lyr, points);
いや〜、チューニングってたのしいですねぇw

